About
About me
Currently a third year math graduate student at Yale University.
Research
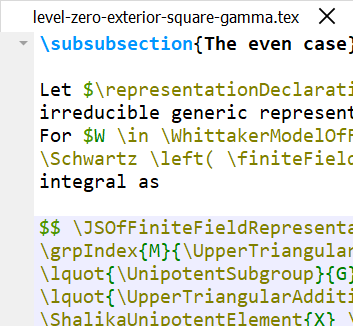
Preprints and publications.
Course notes
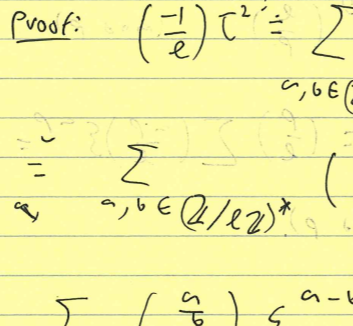
Typed course notes for some courses I have studied.
Blog
My personal blog.
הטיפ היומי
My legacy hebrew blog consisting of C#/.NET programming tips.
WampSharp
My C# implementation of the Web Application Messaging Protocol.